Polígonos
Un polígono es una figura plana compuesta por una secuencia finita de segmentos rectosconsecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices. El interior del polígono es llamado área. El polígono es el casobidimensional del politopo, figura geométrica general definida para cualquier número de dimensiones. A su vez, un politopo de tres dimensiones se denomina poliedro, y de cuatro dimensiones se llama polícoro.
Clasificación de polígonos:
Los polígonos se clasifican por el número de sus lados según la tabla adjunta, o bien por la forma de su contorno o la medida de sus lados:
Por sus lados:
Tres lados: Triangulo
Cuatro lados: Cuadrado.
cinco lados: Pentágono.
Seis lados: hexágono
Siete lados: heptágono.
Ocho lados: Octágono.
Nueve lados: Eneágono
Diez lados: Decágono.
Once lados: Endecágono.
Doce lados: Dodecágono.
Trece lados: Tridecágono.
Catorce lados: Tetradecágono.
Tres lados: Triangulo
Cuatro lados: Cuadrado.
cinco lados: Pentágono.
Seis lados: hexágono
Siete lados: heptágono.
Ocho lados: Octágono.
Nueve lados: Eneágono
Diez lados: Decágono.
Once lados: Endecágono.
Doce lados: Dodecágono.
Trece lados: Tridecágono.
Catorce lados: Tetradecágono.
Quince lados: Pentadecágono.
Un polígono, por la forma de su contorno, se denomina
Simple, si ningún par de aristas no consecutivas se corta.Complejo, si dos de sus aristas no consecutivas se intersecan.
Convexo, si al atravesarlo una recta lo corta en un máximo de dos puntos, es el que tiene todos sus ángulos menores que 180º.
Cóncavo, si al atravesarlo una recta puede cortarlo en más de dos puntos; es el que tiene uno o varios ángulos mayores que 180º.
Equilátero, si tiene todos sus lados iguales.
Equiángulo, si tiene todos sus ángulos iguales.
Regular, si es equilátero y equiángulo a la vez.
Irregular, si tiene sus ángulos y lados desiguales.
Ortogonal o isotético, si todos sus lados son paralelos a los ejes cartesianos
 o
o  .
. Alabeado, si sus lados no están en el mismo plano.
Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.
Por sus ángulos:CONCAVOS: Si un ángulo mide más de 180°.
Si una de sus diagonales es exterior.
CONVEXOS: Todos sus ángulos menores que 180°.
Todas sus diagonales son interiores.
Si una de sus diagonales es exterior.
CONVEXOS: Todos sus ángulos menores que 180°.
Todas sus diagonales son interiores.
Ángulos y diagonales en polígonos convexos
MODELOS MATEMÁTICOS.
Para calcular los ángulos y diagonales en un polígono usamos
modelos matemáticos como son:
Suma de los ángulos = 180°(n-2)
Todas las diagonales que pueden
trazarse desde un vértice = n-3
El numero total de diagonales = n(n-3)/2 = nd/2
Para calcular los ángulos y diagonales en un polígono usamos
modelos matemáticos como son:
Suma de los ángulos = 180°(n-2)
Todas las diagonales que pueden
trazarse desde un vértice = n-3
El numero total de diagonales = n(n-3)/2 = nd/2

Cálculo de áreas en polígonos regulares
Existen diversas fórmulas para calcular el área de un polígono regular, dependiendo de los elementos conocidos.
En función del perímetro y la apotema
El área de un polígono regular, conociendo el perímetro y la apotema es:
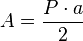
En función del número de lados y la apotema
Sabiendo que:Además , ya que es la mitad de un ángulo central (esto en radianes).Observando la imagen, es posible deducir que:Sustituyendo el lado:Finalmente:Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.
, ya que es la mitad de un ángulo central (esto en radianes).Observando la imagen, es posible deducir que:Sustituyendo el lado:Finalmente:Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.

Lugares geométricos en la circunferencia
Existen varios puntos, rectas y segmentos, singulares en la circunferencia:
Centro: El punto interior equidistante de todos los puntos de la circunferencia;
Radio: El radio de una circunferencia es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio mide la mitad del diámetro. El radio es igual a la longitud de la circunferencia dividida entre 2π.
Diámetro: El diámetro de una circunferencia es el segmento que une dos puntos de la circunferencia y pasa por el centro. El diámetro mide el doble del radio. El diámetro es igual a la longitud de la circunferencia dividida entre π;
Cuerda: La cuerda es un segmento que une dos puntos de la circunferencia. El diámetro es la cuerda de longitud máxima.
Recta secante: Es la línea que corta a la circunferencia en dos puntos;
Recta tangente: Es la línea que toca a la circunferencia en un sólo punto;
Punto de Tangencia: El de contacto de la recta tangente con la circunferencia;
Arco: El arco de la circunferencia es cada una de las partes en que una cuerda divide a la circunferencia. Un arco de circunferencia se denota con el símbolo sobre las letras de los puntos extremos del arco.
Teoremas de ángulos, dentro y fuera de la circunferencia.




.gif)
Modelos matemáticos para determinar área,
perímetro y volumen de la circunferencia
Área
La curva denominada circunferencia encierra en su interior una superficie. Esta superficie se llama área de la circunferencia.
Existe una fórmula muy sencilla que nos permite calcular cuál es el área encerrada dentro de la circunferencia sólo sabiendo cuando mide el radio de la circunferencia.
Llamemos r al radio de la circunferencia, entonces el área de la circunferencia será:
Veamos un ejemplo de como podemos calcular el área de una circunferencia.

En la circunferencia de la imagen expuesta arriba se ve claramente que el área encerrada por la circunferencia es la que está en color blanco. En este caso la variable r toma el valor r=10 cm. El área se calcularía de la siguiente forma:
Nota 1: vemos que las unidades del parámetro r son cm. Podría ser cualquier unidad de medida, como por ejemplo cm, m, mm... u otras unidades como pulgadas, por ejemplo.
Nota 2: las unidades en que sale el área son unidades de longitud al cuadrado al haber multiplicado una distancia por si misma.
Perímetro
Dada una circunferencia, el perímetro de una circunferencia es la longitud de la curva, es decir, la distancia que caminaría una persona que empezara a caminar en un punto de la circunferencia y diera una vuelta alrededor de la circunferencia hasta llegar al punto de partida.
De igual manera que para el área, existe una expresión que nos permite saber la longitud (o perímetro) de la circunferencia sólo conociendo su radio r .
La expresión es la siguiente:
Veámoslo más claro con un ejemplo:
Tomemos la circunferencia del ejemplo anterior, que volvemos a representar a continuación:

De nuevo el parámetro r es r=10 cm.
Aplicando la fórmula explicada anteriormente se obtiene:
Volumen
La fórmula para calcular el volumen de una esfera es: V = (4/3) (π) (r3)
Ejercicio
Calcula el volumen de una esfera cuyo diámetro es de 28 centímetros.

Por ejemplo, digamos que el diámetro es igual a 14. ¿Qué tiene que ver el diámetro con todo esto?. Bueno, da la casualidad de que la mitad del diámetro de un círculo se llama radio.
En este caso, el radio es de 7 (la mitad de 14). Ten en cuenta que si el radio ya está dado, entonces no es necesario dividir el diámetro, ya está hecho. Ahora, sólo tienes que enchufar eso en la fórmula: V = (4/3) (π) (73).
Sabes que 73 = 7x7x7 = 343.
Así que ahora debes tener V = (4/3) (π) (343). Multiplica 343 por pi (3.14), que entonces te dará V = 4/3 (1.077,02). Multiplica 4 con lo del paréntesis (por 1.077,02). Ahora vas a obtener V = 4308.08 / 3. Divide 4,308.08 por 3 y finalmente tendrás tu respuesta, que es V = 1436.
Esta es la fórmula para calcular el volumen de una esfera. Recuerda siempre tener cuidado con las unidades de medida en la que haces los cálculos, y la unidad de medida cubica del resultado final.


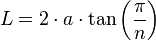


No hay comentarios:
Publicar un comentario